When I started writing my PhD, I began with a chapter on the history of parametric architecture. I was really interested in when the concept of 'parametric' design was first developed and how it took off. This proved to be a big diversion (my PhD wasn't about the history of parametric design!). So I ended up deleting the chapter. But now that I have finished my thesis, I was going back through my notes and rediscovered this chapter. A five-thousand-word B-side. Hopefully, others find this history more useful than I did. And for all the Spanish speakers out there: Version en español.
Parametric Origins
The term parametric originates in mathematics, but there is debate as to when designers initially began using the word. David Gerber (2007, 73), in his doctoral thesis Parametric Practice, credits Maurice Ruiter for first using the term in a paper from 1988 entitled Parametric Design1. 1988 was also the year Parametric Technology Corporation (founded by mathematician Samuel Geisberg in 1985) released the first commercially successful parametric modelling software, Pro/ENGINEER (Weisberg 2008, 16.5). But Robert Stiles (2006) argues that the real provenance of parametric was a few decades earlier, in the 1940s’ writings of architect Luigi Moretti (Bucci and Mulazzani 2000, 21).

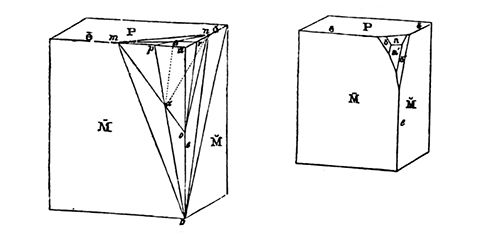
A model of stadium N by Luigi Moretti. Exhibited at the 1960 Parametric Architecture exhibition at the Twelfth Milan Triennial. The stadium derives from a parametric model consisting of nineteen parameters (Bucci and Mulazzani 2000, 114).
Moretti (1971, 207) wrote extensively about “parametric architecture,” which he defines as the study of architecture systems with the goal of “defining the relationships between the dimensions dependent upon the various parameters.” Moretti uses the design of a stadium as an example, explaining how the stadium’s form can derive from nineteen parameters concerning things like viewing angles and the economic cost of concrete (Moretti 1971, 207). Versions of a parametric stadium designed by Moretti were presented as part of his Parametric Architecture exhibition at the Twelfth Milan Triennial in 1960 (Bucci and Mulazzani 2000, 114). In the five years following the exhibition, between 1960 and 1965, Moretti designed the Watergate Complex, which is “believed to be the first major construction job to make significant use of computers” (Livingston 2002). The Watergate Complex is now better known for the burglary that took place there, and Moretti is “scarcely discussed” (Stiles 2006, 15) – even by the many architects who today use computers to create parametric models in the manner Moretti helped pioneer.
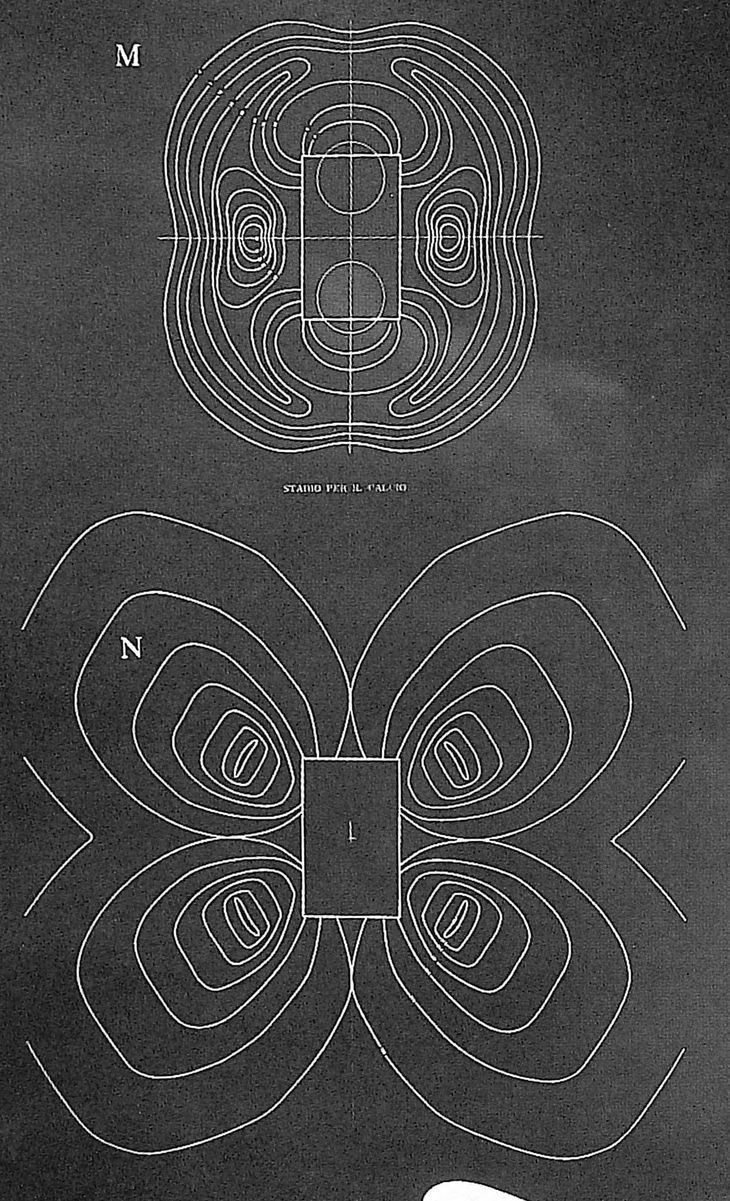
The plans for stadium version M and N showing the “equi-desirability” curves (Bucci and Mulazzani 2000, 114).
The term parametric has a long history in mathematics. The earliest examples I can find of parametric being used to describe three-dimensional models comes almost one hundred years before Moretti’s writings. One example is James Dana’s 1837 paper On the Drawing of Figures of Crystals (other examples from the period include: Leslie 1821; Earnshaw 1839)2. In the paper, Dana explains the general steps for drawing a range of crystals and provisions for variations using language laced with parameters, variables, and ratios. For instance, in step eighteen, Dana tells the reader to inscribe a parametric plane on a prism:
If the plane to be introduced were 4P2 the parametric ratio of which is 4:2:1, we should in the same manner mark off 4 parts of e, 2 of ē and 1 of ë.
Dana 1837, 42
In this quote, Dana is describing the parametric relationship between three parameters of the plane (4:2:1) and the respective division of lines e, ē, and ë. The rest of the twenty-page paper possesses similar statements that explain how various parameters filter through long equations to affect the drawing of assorted crystals. Dana’s crystal equations resemble those that would be used by architects 175 years later to develop parametric models of architecture – architecture that has a “crystalline splendour” according to Moretti (1957, 184).
Instances of James Dana’s crystal drawings showing the impact of changing the edge chamfer ratio (Dana 1837, 43).
Parametric is given no particular significance in Dana’s writing. Dana does not describe his drawings as parametric, nor does he claim, as Schumacher (2009a, 15) later would, that designing with parametric equations “justifies the enunciation of a new style in the sense of an epochal phenomenon.” Instead, Dana uses parametric in its original mathematical sense, a word given no more emphasis than other technical terms like parallel, intersection, and plane.
When used by Dana in 1837, or by mathematicians today, parametric signifies what the Concise Encyclopedia of Mathematics calls a “set of equations that express a set of quantities as explicit functions of a number of independent variables, known as ‘parameters’” (Weisstein 2003, 2150)3. This definition sets forth two critical criteria:
- A parametric equation expresses “a set of quantities” with a number of parameters4.
- The outcomes (the set of quantities) are related to the parameters through “explicit functions”5. This is an important point of contention in later definitions since some contemporary architects suggest that correlations constitute parametric relationships.
An example of a parametric equation is the formulae that define a catenary curve:
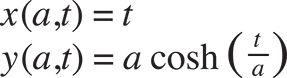
These two formulae meet the criterion of a parametric equation. Firstly, they express a set of quantities (in this case an x quantity and a y quantity) in terms of a number of parameters (a, which controls the shape of the curve; and t, which controls where along the curve the point occurs). Secondly, the outcomes (x & y) are related to the parameters (a & t) through explicit functions (there is no ambiguity in the relationships between these variables). This technical mathematical definition is the origin of the term parametric: a set of quantities expressed as an explicit function of a number of parameters.
Analogue Parametric: Gaudí
Aside from Dana’s parametric crystal drawings in 1837, there are many other cases of early ninetieth-century science entangled with the mathematics of parametric representations. An example from the period includes Sir John Leslie (1821, 390), in his book on geometric analysis, proving the self-similarity of catenary curves using “parametric circles”. Another example is Samuel Earnshaw (1839, 102), who wrote about “hyperbolic parametric surfaces” deformed by lines of force in a paper that gave rise to Earnshaw’s theorem. These examples of expressing geometry with parametric equations are two of many from the period, a period well before Antoni Gaudí first began designing architecture with parametric catenary curves and parametric hyperbolic paraboloids at the end of the ninetieth century.
It is impossible to know whether Gaudí was directly influenced by the various scientists and mathematicians who had earlier used parametric equations to define geometry. Mark Burry (2007a, 11), the current executive architect of Gaudí’s Sagrada Família, says there is “virtually nothing written by Gaudí himself about the motivations, theories and practice that pushed him to stretch the limits”. It is known that Gaudí’s university curriculum included, among other things, “advanced mathematics, general physics, natural science, and descriptive geometry” (Català 2007, 81). Gaudí’s deep understanding of mathematics underlies his architecture, especially his later architecture, which almost exclusively consists of mathematical ruled surfaces – helicoids, paraboloids, and hyperboloids – parametrically associated together with ruled lines, booleans, ratios, and catenary arches (J. Burry and M. Burry 2010, 35-39; M. Burry 2011, 144). Whether or not Gaudí knew of the earlier work defining geometry with parametric equations, Gaudí certainly employed models underpinned by parametric equations when designing architecture.

Hooke’s (1675, 31) anagram of the hanging chain model. At the time, anagrams were a common way to claim the first publication of an idea before the results were ready to publish.
The use of parametric equations can be seen in many aspects of Gaudí’s architecture but is perhaps best illustrated by his use of the hanging chain model (M. Burry 2011, 152-70). The hanging chain model originates from Robert Hooke’s (1675, 31) anagram “abcccddeeeeefggiiiiiiiiillmmmmnnnnooprrsssttttttuuuuuuuuu”, which unscrambled and translated from Latin reads “as hangs the flexible line, so but inverted will stand the rigid arch” (Heyman 1995, 7). Gaudí used this principle to design the Colònia Güell Chapel by creating an inverted model of the chapel using strings weighed down with birdshot (M. Burry 2007b). Because of Hooke’s principle, the strings would always settle into a shape that, when inverted, would stand in pure compression. The hanging chain model has all the components of a parametric equation. There are a set of independent parameters (string length, anchor point location, birdshot weight) and there are a set of outcomes (the various vertex locations of points on the strings) that derive from the parameters using explicit functions (in this case Newtons laws of motion). By modifying the independent parameters of this parametric model, Gaudí could generate versions of the Colònia Güell Chapel and be assured the resulting structure would stand in pure compression.
.](/img/tragwerkslehre082_Page_3-zJCTvAg6MU-730w.jpeg)
Inside Gaudí’s hanging model for the Colònia Güell. Via.
Compared to the earlier use of parametric equations by scientists and mathematicians, the critical innovation of Gaudí’s hanging chain model is that it automatically computes the parametric outcomes. Rather than manually calculating the outputs from the catenary curve’s parametric formula, Gaudí could automatically derive the shape of catenary curves through the force of gravity acting on strings. This method of analogue computing was enlarged by Frei Otto to include, amongst other things, minimal surfaces derived from soap films and minimal paths found through wool dipped in liquid.
Otto (1996) calls designing with these models form finding, which is a phrase that foregrounds the exploratory nature of parametric modelling. In Gaudí’s case, the hanging chain model facilitates exploration of form both by constraining Gaudí to structurally sound shapes and by automatically deriving these shapes whenever Gaudí modifies the parameters of the model. This forms an essential component of the parametric modelling dogma for architects, namely the utility of parametric models lies in the exploration of outcomes. The original mathematical definition of parametric remains unmodified, these analogue parametric models all have a set of quantities expressed as an explicit function of a number of independent parameters, however this is complemented by a utilitarian emphasis on exploring the possibilities offered by the model.
Sketchpad
The digitisation of computation facilitated calculations not possible with Gaudí and Otto’s analogue parametric models. In much the same way Gaudí and Otto used physical laws to speed up the calculation of select parametric equations, Ivan Sutherland sought to use computers to speed up the calculation of any parametric equation. Sutherland (1963, 8) wanted to create a system that enabled “a man and a computer to converse” (8). At a time when computers ran in batch mode, and when programming felt like “writing letters” (Sutherland 1963, 8), the concept of an interactive digital model was a bold vision. Sutherland harnessed the computational power of the TX-2 computer to create Sketchpad, the first interactive computer-aided design program. Using a light pen, a designer could draw lines and arcs, which could then be related to one another with what Sutherland (1963, 18) called atomic constraints. Sutherland never used the word parametric in his writing, but the atomic constraints have all the essential properties of a parametric equation: each constraint has a set of outcomes expressed as an explicit function of a number of independent parameters. Unlike with Gaudí and Otto’s models, these parametric equations are not bound to physical laws, so they can compute relationships like parallel, orthogonal, and coincident.
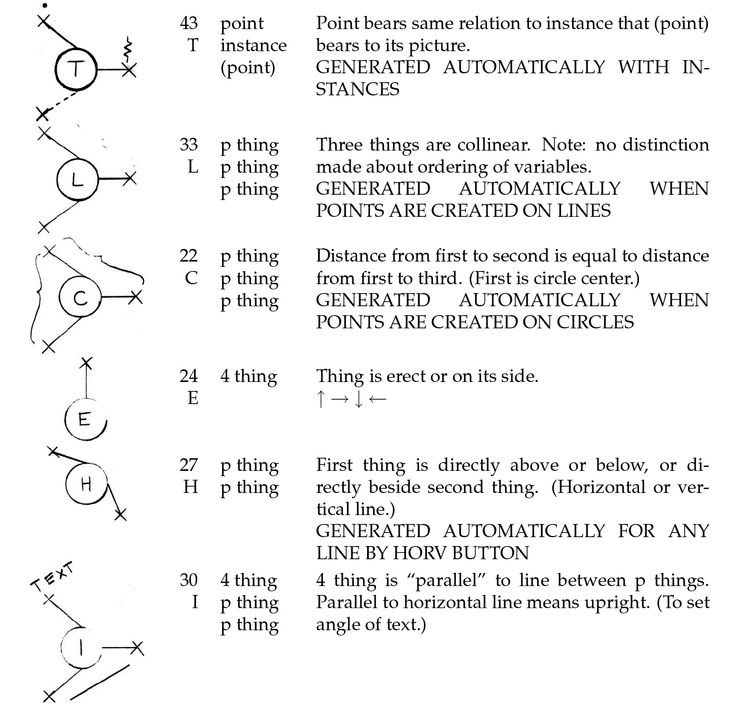
Sutherland’s (1963, ‘Appendix A’) diagram of six of the seventeen atomic constraints in Sketchpad. Each constraint has a set of input variables and an explanation of the explicit functions that transform the variables into the desired outputs.
Sketchpad offered a new way to explore parametric equations. As with Gaudí and Otto’s models, designers could explore variations by modifying parameters and having Sketchpad automatically recalculate and redraw the geometry. But in Sketchpad designers were also free to modify the relationships of the model, which would also cause the recalculation and redrawing of geometry. Thus the architect’s control of Sketchpad, as with most parametric modelling software, is not only through the parameters of the model but also through the model’s underlying relationships.
The Computer Age
In the froth of invention surfaced by the electronic computer, no one – not even Sutherland – realised the impact parametric design would have on architectural practice over the next fifty years. The 1960s and 1970s were an optimistic period in computing and Sutherland’s vision of computers replicating drafting tables was almost pessimistic compared to his contemporaries’ bullish calls for: automated architects (Whitehead and Elders 1964; Cross 1977), designed aided by evolution (Frazer 1995 [with projects from 1966]), self-replicating geometry and cellular automata (Neumann 1951), computer-aided design (Coons 1963 [Sutherland’s supervisor]; Mitchell 1977), shape grammars (Stiny and Gips, 1972) and Bézier curves (independently developed by Casteljau in 1959 and by Bézier in 1962 [Böhm, Farin, and Kahmann 1984, 6]).

Itek’s Electronic Drafting Machine (above) and sample drawing (below). The setup cost US$500,000 per seat in 1962 – approximately equivalent to US$3.5 million in 2012 (Weisberg 2008, ch. 6.6).
Much of this innovation failed to take root in architectural practices. Early commercial systems like Itek’s Electronic Drafting Machine cost the equivalent of US$3.5 million per seat when they were released in 1962, which was a cost bearable only by select automotive and aeronautical companies (Weisberg 2008, chap. 6). Twenty years later, in August 1982, a time when computers were becoming affordable enough for some people to own a personal computer, AutoCAD was released and quickly rose to dominate the fledgling computer-aided design industry (Weisberg 2008, chap. 8). Gone were the curves, the artificial intelligence, and the self-replicating geometries, which were replaced in AutoCAD with commands enabling the designer to explicitly draft two-dimensional lines on screen using a keyboard rather than a pen. Eighteen versions later, in AutoCAD2010, parametric functionality was introduced (forty-three years after Sketchpad) and pronounced in the press release, “a groundbreaking new capability” (Autodesk 2009). Sometimes it takes a while to realise the impact concepts like parametric design will have on practice.
AutoCAD2010’s groundbreaking new parametric modelling features were present in software decades ago. In 1985, the former mathematics professor Samuel Geisberg founded Parametric Technology Corporation. They shipped what would become the first commercially successful parametric software, Pro/ENGINEER, in 1988. Like with Sketchpad, users could associate parts of the Pro/ENGINEER geometry together using various parametric equations. Unlike Sketchpad, the geometry was three-dimensional rather than two-dimensional and changes could propagate over many different drawings created by many different users. During an interview with Industry Week in 1993, Geisberg succinctly expressed the original motivations of Pro/ENGINEER and captured, to a large extent, the motivations of parametric modelling:
The goal is to create a system that would be flexible enough to encourage the engineer to easily consider a variety of designs. And the cost of making design changes ought to be as close to zero as possible. In addition, the traditional CAD/CAM software of the time unrealistically restricted low-cost changes to only the very front end of the design-engineering process.
Geisberg quoted in: Teresko 1993, 28
Geisberg makes two salient points. The first is that parametric modelling should enable designers to explore “a variety of designs” (Teresko 1993, 28). This is made possible in Pro/ENGINEER both through the manipulation of parameters and through the manipulation of the model’s underlying relationships. His second point is that parametric models allow choices to be made later in the design process, a point I will return to later in this chapter since deferred decisions continue to be an alluring possibility of parametric modelling.
.](/img/catia-1-A_NPC1mjAR-500w.jpeg)
Guggenheim in CATIA. Via.
In 1993 Dassault Systèmes incorporated many of Pro/ENGINEER’s parametric features into CATIA v4 (Weisberg 2008, 13:32). At the time, Gehry Partners was employing Rick Smith, a CATIA expert originally from the aerospace industry, to help realise geometrically challenging architecture projects like the Barcelona Fish (1991) and the Guggenheim Museum in Bilbao (1993-97). This work forms the basis of Gehry Partners’ sister company, Gehry Technology (incorporated in 2001), which went on to release the parametric modelling software Digital Project in 2004. Digital Project takes CATIAv5 and wraps it with tools tailored to architects, in particular architects trying to rationalise geometry as characteristically complicated as Gehry’s own. Much of Digital Project relies on CATIAv5’s parametric engine, an engine that enables architects to revise the parameters and equations defining their geometry in much the same way engineers have been doing with Pro/ENGINEER.
By the time Digital Project was released in 2004, most architects had begrudgingly replaced their drawing boards with personal computers. Only a handful of architecture firms were producing geometry intricate enough to warrant using Digital Project, with the vast majority instead using computers simply to draft and coordinate drawing sets. While some architects stuck to AutoCAD and its numerous competitors, others chose to adopt specialist building modelling software like Revit and ArchiCAD.
Revit Technology Corporation was founded by former Parametric Technology Corporation developers who aspired to create the “first parametric building modeler for architects and building design professionals” (RTC 2000a). Before being acquired by Autodesk in 2002, the Revit website used to greet visitors with a fairly oblique definition of parametric:
.](/img/revit-1-KTcW9BEOrt-727w.jpeg)
Revit homepage as of 10 May 2000. Via.
In essence, the authors of Revit define parametric as an object based on parametric equations that the designer can adjust for particular circumstances. In later versions of the website, they explain how a designer might adjust the pitch of the roof and how Revit “in turn, will ‘revit’ (or revise instantly) all plans, elevations, sections, schedules, dimensions and other elements” (RTC 2001). While Revit and its ilk undoubtedly use parametric equations for these automatic revisions, unlike fully-fledged parametric modelling software such as Pro/ENGINEER, CATIA, or even Sketchpad, the parametric relationships of Revit are hidden behind the interface. The focus is on using parametric models rather than creating them. After Revit was acquired by AutoDesk, the rhetoric around parametric modelling ceased and they coined (some say appropriated) the name Building Information Modelling (BIM) to denote their brand of design (Weisberg 2008, 8:47). In doing so, they distinguished BIM from parametric modelling by emphasising the management of information (parameters), as opposed to the management of the parametric model itself. Therefore, while the majority of architecture firms may never use overtly parametric software like Digital Project or Pro/ENGINEER, most – often without even considering it – use parametric equations in some capacity to model their buildings.
Parametric modelling has also made its way into projects through the scripting interfaces of software packages. Scripting interfaces allow designers to write code to automate parts of the software. The developers of software like AutoCAD, even back in 1982 realised that including a scripting interface allowed them to “avoid lots of custom coding and application-specific stuff [they would] otherwise get asked for” (Walker 1994, 115). Ten years later, in 1992, when Mark Burry (2011, 28-29) wanted to model hyperbolas parametrically for the Sagrada Família, rather than ask Autodesk to include a hyperbola function in AutoCAD, he used the AutoCAD scripting interface to develop his own. Burry’s script had three input parameters: an origin point, a minimum point, and an asymptote point. These parameters feed through a number of explicit equations (written in AutoLISP code) to output a hyperbola. The script, with its input parameters, explicit functions, and outputs, is an archetypal embodiment of the mathematical definition of parametric. Ipek Dino (2012, 210) has argued scripts are inherently parametric, noting that “parametric systems are principally based on algorithmic principles” since “an algorithm takes one value or a set of values as input, executes a series of computational steps that transform the input, and finally produces one value or a set of values as output”. Thus the scripting interfaces accessible in most software packages are innately predisposed to creating parametric models.
.](/img/ExplicitHistory-xUPU8vc6pf-725w.jpeg)
First version of Explicit History, later known as Grasshopper. Via.
Textual scripting interfaces have not developed significantly since the early days of AutoCAD. Instead, the past decade has seen the emergence of a new type of scripting interface, the visual interface. Visual programming involves representing programs not as text but rather as diagrams. Two notable precedents from the 1990s include MAX/MSP, which is popular with musicians, and Sage (later Houdini), which is popular with visual effects artists. Architects got their first visual-scripting language when Robert Aish, then working for Bentley Systems, started quietly beta testing Generative Components with select architecture firms in 2003. Robert McNeel & Associates, after trying unsuccessfully to license Generative Components, assigned developer David Rutten to make their own version (Tedeschi 2010, 28). Released in 2007 as Explicit History, Rutten later dubbed his visual scripting interface Grasshopper. Both Grasshopper and Generative Components are based around graphs (a mathematical name for a type of flowchart) that map the flow of relations from parameters, through user-defined functions, usually concluding with the generation of geometry. Changes to parameters or the model’s relationships cause the changes to propagate through the explicit functions to automatically redraw the geometry. As such, they are yet another way to create a parametric model.
Conclusion
Only in the last decade has parametric modelling gone from being a mathematical method employed by Gaudí, Otto, Sutherland, and some engineers, to being a regular part of architectural practice. While in mathematics parametric signifies a set of quantities expressed as an explicit function of a number of independent parameters, in architecture the term parametric is often accompanied by a utilitarian need to explore the possibilities of the model. This exploration is facilitated both through the modification of model parameters and through the modification of model relationships. In the present day, parametric modelling is no longer the exclusive domain of overtly parametric tools like CATIA and Pro/ENGINEER. Instead, parametric equations quietly drive many BIM tools, they manifest in textual scripting languages, and they are exposed by graph-based visual scripting interfaces. Parametric modelling is present, in some form, on most contemporary architecture projects. It is this rapid expansion in the application of parametric modelling that has understandably led to some confusion over its meaning.
Endnotes
1:Gerber claims Ruiter’s paper was published in Advances in Computer Graphics III (1988). When I looked at this book, none of the papers were titled Parametric Design and none of the papers were written by Ruiter (he was the editor not writer). As best I can tell, there never was a paper titled Parametric Design produced in 1988. The first reference I can find to Ruiter’s supposed paper is in the bibliography of Javier Monedero’s 1997 paper, Parametric Design: A Review and Some Experiences. It is unclear why Monedero included the seemingly incorrect citation since he never made reference to it in the text of his paper. As an aside: the word parametric does appear four times in Advances in Computer Graphics III – on pages 34, 218, 224, & 269 – which indicates that the use of parametric in relation to design was not novel at the time.
2:By searching for parametric in Google Ngrams (http://books.google.com/ngrams/) I was able to find the earliest occurrences of parametric from the collection of books that Google has scanned. Google has scanned only a limited collection of books so there may be even earlier examples that were not returned in these searches. Nevertheless, Dana’s writings in 1837 significantly predate any claims I have found in various histories of parametric design as to the first use of the term parametric in relation to drawing.
3:This definition is consistent with definitions in other mathematical dictionaries and encyclopedias. I have chosen to cite from the Concise Encyclopedia of Mathematics as the editor, Eric Weisstein (who is also the chief editor of Wolfram Mathworld) is considered an authoritative source.
4:Parameter can have a number of meanings, even when used by mathematicians. The grammarian James Kilpatrick (1984, 211-12) quotes a letter he received from R. E. Shipley: “With no apparent rationale, nor even a hint of reasonable extension of its use in mathematics, parameter has been manifestly bastardized, or worse yet, wordnapped into having meanings of consideration, factor, variable, influence, interaction, amount, measurement, quantity, quality, property, cause, effect, modification, alteration, computation etc., etc. The word has come to be endowed with ‘multi-ambiguous non-specificity’.” In the Concise Encyclopedia of Mathematics (Weisstein 2003, 2150), the term parameter used in the context of a parametric equation means an “independent variable.” That is, a variable whose value does not depend on any other part of the equation (the prefix para- being Greek for beside or subsidiary).
5:An explicit function is a function whose output value is given explicitly in terms of independent variables. For example, the equation x_∙_x + y_∙_y = 1 is the implicit function for a circle. The function is implicit since the outputs (x and y) are defined in terms of one another. To make the function explicit, x and y have been defined in terms of an independent variable. Thus, the explicit function of a circle becomes: x = cos(t), y = sin(t). By a similar token, saying that ‘x is roughly twice as large as t’ is not an explicit function since there is ambiguity regarding the exact relationship between the variables t and x (the relationship is non-explicit).
Bibliography
Autodesk. 2009. “Autodesk Takes 3D Design and Documentation to Next Level with AutoCAD 2010.” Published February 5. http://usa.autodesk.com/adsk/servlet/item?siteID=123112&id=13315136.
Böhm, Wolfgang, Gerald Farin, and Jürgen Kahmann. 1984. “A Survey of Curve and Surface Methods in CAGD.” Computer Aided Geometric Design 1 (1): 1-60.
Burry, Jane, and Mark Burry. 2010. The New Mathematics of Architecture. London: Thames and Hudson.
Burry, Mark. 2007a. “Setting the Scene.” In Gaudí Unseen: Completing the Sagrada Famíla, edited by Mark Burry, 10–58. Berlin: Jovis.
Burry, Mark. 2007b. “Innovative Aspects of the Colònia Güell Chapel Project.” In Gaudí Unseen: Completing the Sagrada Famíla, edited by Mark Burry, 59-61. Berlin: Jovis.
Burry, Mark. 2011. Scripting Cultures. Chichester: Wiley.
Bucci, Federico, and Marco Mulazzani. 2000. Luigi Moretti: Works and Writings. New York: Princeton Architectural Press.
Català, Claudi. 2007. “Gaudí, the Geometer.” In Gaudí Unseen: Completing the Sagrada Famíla, edited by Mark Burry, 81-85. Berlin: Jovis.
Coons, Steven. 1963. “An Outline of the Requirements for a Computer-aided Design System.” In AFIPS Conference Proceeding: 1963 Spring Joint Computer Conference, 299-304. London: Cleaver-Hume Press.
Cross, Nigel. 1977. The Automated Architect. London: Pion.
Dana, James. 1837. “On the Drawing of Figures of Crystals.” The American Journal of Science and Arts 32: 30-50.
Dino, Ipek. 2012. “Creative Design Exploration by Parametric Generative Systems in Architecture.” METU Journal of Faculty of Architecture 29 (1): 207–224.
Earnshaw, Samuel. 1839. “On the Nature of the Molecular Forces which Regulate the Constitution of the Luminiferous Ether.” Transactions of the Cambridge Philosophical Society 7: 97-112.
Frazer, John. 1995. An evolutionary Architecture. London: Architectural Association.
Gerber, David. 2007. “Parametric Practices: Models for Design Exploration in Architecture.” PhD dissertation, Harvard University.
Heyman, Jacques. 1995. The Stone Skeleton: Structural Engineering of Masonry Architecture. Cambridge: Cambridge University Press.
Hooke, Robert. 1675. A Description of Helioscopes, and Some Other Instruments. London: Royal Society.
Kilpatrick, James. 1984. The Writer’s Art. Kansas City: Andrews, McMeel, and Parker.
Leslie, John. 1821. Geometrical Analysis and Geometry of Curve Lines. Second edition. Edinburgh: W. & C. Tait.
Livingston, Mike. 2002. “Watergate: The name that branded more than a building.” Washington Business Journal, 17 June.
Mitchell, William. 1977. Computer-Aided Architectural Design. New York: Petrocelli/Charter.
Monedero, Javier. 1997. “Parametric Design. A Review and Some Experiences.” In Challenges of the Future: 15th eCAADe Conference Proceedings, edited by Bob Martens, Helena Linzer, and Andreas Voigt.
Moretti, Luigi. 1971. “Ricerca Matematica in Architettura e Urbanisticâ.” Moebius IV no. 1, 30-53. Republished in: Federico Bucci and Marco Mulazzani. 2000. Luigi Moretti: Works and Writings. New York: Princeton Architectural Press. Citations refer to the 2000 publication.
Neumann, John. 1951. “General and Logical Theory of Automata.” In Cerebral Mechanisms in Behavior: The Hixon Symposium, edited by Lloyd Jeffress, 1-41.
Otto, Frei, and Bodo Rasch. 1996. Finding Form: Towards an Architecture of the Minimal. Stuttgart: Axel Menges.
RTC (Revit Technology Corporation). 2000a. “Revit Technology Corporation Launches Industry’s First Parametric Building Modeler.” Press release, April 5. Waltham.
RTC (Revit Technology Corporation). 2000b. “Revit Technology Corporation ‑ Product.” http://revit.com/cornerstone/index.html. Copy archived May 10, 2000. http://web.archive.org/web/20000510111053/http://revit.com/cornerstone/index.html.
RTC (Revit Technology Corporation). 2001. “Technical Overview.” http://www.revit.com/cornerstone/content_technical.html. Copy archived February 6, 2001. http://web.archive.org/web/20010206204349fw_/http://www.revit.com/cornerstone/content_technical.html.
Ruiter, Maurice, ed. 1988. Advances in ComputerGraphics III. Berlin: Springer-Verlag.
Schumacher, Patrik. 2009a. “Parametricism: A New Global Style for Architecture and Urban Design.” Architectural Design 79 (4): 14–23.
Stiny, George, and James Gips. 1972. “Shape Grammars and the Generative Specification of Painting and Sculpture.” In Proceedings of IFIP Congress 1971, edited by C. V. Freiman, John Griffith, and J. L. Rosenfeld, 125–135. Amsterdam: North Holland Publishing.
Sutherland, Ivan. 1963. “Sketchpad: A Man-Machine Graphical Communication System.” PhD dissertation, Massachusetts Institute of Technology.
Stiles, Robert. 2006. “Aggregation Strategies.” Masters dissertation, University of Bath.
Tedeschi, Arturo. 2010. “Interview with David Rutten.” MixExperience: Tools. Accessed November 18, 2012. http://content.yudu.com/Library/A1qies/mixexperiencetoolsnu/resources/index.htm.
Teresko, John. 1993. “Parametric Technology Corp.: Changing the way Products are Designed.” Industry Week, December 20.
Walker, John, ed. 1994. The Autodesk File: Bits of History, Words of Experience. Fourth edition. Self published. Earlier editions published in 1989 by New Riders Publishing.
Weisberg, David. 2008. “The Engineering Design Revolution: The People, Companies and Computer Systems that Changed Forever the Practice of Engineering.” Accessed July 23, 2011. http://www.cadhistory.net.
Weisstein, Eric. 2003. CRC Concise Encyclopedia of Mathematics. Second edition. Boca Raton: Chapman & Hall/CRC.
Whitehead, B., and M. Z. Elders. 1964. “An approach to the Optimum Layout of Single Story Buildings.” Architects Journal 139 (25): 1373-1380.
Diederik Veenendaal
Great text and very informative! The parts about Moretti and Dana are completely new to me. I love your writing style and I appreciate all the comments on how the term 'parametric' can be defined, or has changed through its use or has been hijacked, depending on how you look at it. Especially juxtaposing Dana and Schumacher, and their use of the word, is interesting. Glad you posted it.
Good luck in New York!
Daniel
Thank you Diederik. In my thesis I have a whole section that looks at how the word 'parametric' has been used in the discourse. There is so much disagreement over this word, which, more than anything, is an indication of how how important parametric modelling is becoming.
Miguel Angel Jimenez
Really great text... you provide a clever clue so we can have a better understanding of what are we really doing when designing... priceless...
Ben Regnier
A very complete history - love the detail on anagrams in Hooke's time(!) As long as we are discussing the meaning of the term 'parametric' in architecture, I would like to bring up a related mathematic term that is also used in architectural parametrics: "constraints." In math it's often used side by side as an equivalent word (as in parameters/constraints). I would argue that in BIM the concept of a parameter as constraint is the basic building block, and that limitations are more important than capabilities. Constraints are usually related to a specific field or arena: hanging chain models use the constraints of physics; BIM uses the constraints of building construction and documentation, etc. Understanding parametric systems as "guide rails" more than an engine of automatic changes provides a different angle on the same subject, one that might provide more clues into its utility in practice.
Daniel
I find the anagrams fascinating. Apparently it was quite common in the seventeenth century to passive-aggressively send other scientists an anagram of your discovery, leaving them to agonise over unscrambling it. I love this story from This American Life about Kepler discovering Mar's moons by misinterpreting Galileo's anagram: http://www.thisamericanlife.org/radio-archives/episode/475/send-a-message?act=0#play
Parametric systems as guide rails is a nice way to put it. I don't often put it in these terms but I think it is a really valuable complementary perspective. Axel Kilian's Design Exploration through Bi-directional Modelling of Constraints really nicely explores how constraints can be viewed as positive (even necessary) to the design process.
Adrian Williamson
Daniel, great article/ thesis, I wrote a dissertation back in 1999/2000 on digital architecture and just scratched the surface of parametrics I was more concerned with interoperability, did do a bit of work looking at Autodedk Inventor & Revit pre Autodesk era. Using ArchiCAD these days but great to read about how these progs all came about.
Thanks Adrian
Daniel
Thank you for stopping by Adrian. It is crazy to think of how much the technology has changed even in the 13 years between 2000 and now. When writing my thesis I was always a little worried my work would be rendered completely irrelevant by some new technological development. But I guess some things don't change, interoperability is still a huge issue for the industry.
Sweta
THIS WAS SIMPLY awesome. IM so glad you assorted this onformation. I needed all of it for this presentation I had to make BUt not only that, it HAS truly inspired me to research on parametric architecture. THANK YOU SOOOOO MUCH!!! :D
Melissa
Thanks Daniel, fantastic content, rendered beautifully. I've been searching for this for years, in fact I stumbled on your site originally (about 5-6 years ago) after typing parametric architecture into google. Especially loved the 'hanging chain model' section; if I ever start a band, that will be the name. best Melissa
Daniel
Haha. That'd quickly become the only band I'd play in studio -- someone definitely needs to make this happen! Actually I just googled 'hanging chain band' and got this. It's all I am ever going to listen to now when I make my hanging chains.
shaghayegh
it was very helpful...thanks
Jeremy Merrill
Thank you for putting this out there. It was very informative.
Engineering dude
I had a 10,000 word essay on parametric modeling... this helped me alot
Daniel
Glad to hear it engineering dude! Hope you ace the essay.
Daniel KA
Highly useful, thanks!
John H
Hi Daniel, hope you're well.
I returned to this piece recently and have seen a lot of it has now made it onto Wikipedia. https://en.wikipedia.org/wiki/Parametric_design
I worry about this terminology... Isn't the term 'parametric design' about the use of explicit parametric equations, whereas form-finding methods are outside of this scope in that they include iterative loops?
For example, an n-body simulation is an example of applying Newton's 2nd law iteratively (using finite difference), but the results are far from being what one would call a 'parametric design'. Indeed, any difference equation (such as the logistic map) is not a parametric equation.
I would argue that the term 'parametric design' be limited to parametric equations like Sutherland showed, and not include cycles, feedback loops, chaos, etc...
Is this definition of parametric design too narrow in your opinion? The term 'generative design' is perhaps wider in scope. See debate here: http://www.reneepuusepp.com/what-is-generative-design/ Of course Grasshopper (for example) has now started to embrace cycles of late.
Of course, then there's 'associative', 'algorithmic' and 'computational' to discuss.
I feel a Venn diagram coming on!
Be interested to hear your thoughts.
Thanks, John.
Daniel
Great to hear from you again John!
This blog post came from an early draft of my thesis. When writing my thesis I spent ages deciding whether or not to use the term 'parametric'. At RMIT there was a period where we used the term 'flexible model' but I think it is hard to get people to change their vocabulary. So, for better or for worse, I used the term 'parametric' because it is a term that people frequently use. I was just super careful to define its meaning and avoid schumacher's attempt to co-opt it.
Like you say, there are many other terms we could use that better describe what we do. I'm personally a fan of 'computational design'. I think it'd make a fantastic blog post to list all the various terms and provide definitions for them!
Daniel
John H
Thanks Daniel,
Makes sense. I had a similar dilemma and opted for the 'parametric' term in my thesis whilst trying my best to define it.
The reason this came up again is that in architectural schools in the UK at least, the dreaded 'parametricism' term is on the increase.
I see it as my duty to educate the students that parametric design is something different (i.e. not an all encompassing fascistic architectural style!), although as its not rigidly defined itself in the community this is kind of the problem.
I'll get working on that Venn diagram!
John.
Yara
Firstly, I want to thank you sooooo much for putting this out there. It is very helpful. I would like to ask your permission to use this information in my thesis, It's about Parametric design and how to apply it in the field of Interior Design.
Daniel
Hey Yara, it's awesome that you found this post useful! You're more than welcome to quote from this article in your thesis as long as it's cited. Best of luck for your submission!
Yara
Daniel, I couldn't express my gratitude to you. Sure everything will be cited. Thank you very much.
Fernando Alonso
Thank you very much for this post, I am starting my Phd in this topic, it was really helpful, I have translated the article and post it in my web http://fernandoalonsoarchitect.blogspot.com.es/2017/01/historia-del-diseno-parametrico.html // hope you like! LOVE
Daniel
Hey Fernando, this is really cool! Thanks for taking the time to translate the article, it must have taken ages. I'll add a link to the translation so others can find it. Best of luck for the PhD!
ZAKARIA
i just have a question about some of old pattern if it includ parametric or no because i am really see this pattern a part of parametric design based on the same equation that used in grasshopper.
Jesus Diaz
Hi! My name is Jesus I´m from México, this is an amazing investigation you have here. Right now Im doing a thesis of how parametric can or should help to conservate the heritage of differents buildings and this come to good to help me and to talk about. Thank you so much for this great article.
Jesus Diaz
Sebastião
Realidade evolutiva do design apaixonante por revelar raízes do conhecimento. Top mind
Montserrat G.Maya
Very interesting article, download your thesis to deepen on the subject. I came here as a suggestion and additional material from a BIM course to delve into how all this parametric started. They highly recommended the video that you have in the publication but that is not available today, is it possible to see it on some other platform or link that you can share with me? I have taken a walk to see other of your publications, I will be following you, thank you very much for all the information shared!
Daniel Davis
Thanks for letting me know Montserrat! I've updated the article with a new link to the Sutherland Sketchpad video.